| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 히스토그램
- 밑바닥부터 시작하는 딥러닝2
- 결정계수
- 텐서플로2와 머신러닝으로 시작하는 자연어처리
- 오래간만에 글쓰네
- 최소자승법
- 머신러닝
- 모두의 딥러닝
- 군집화
- student t분포
- 자연어 처리
- numpy
- 밑바닥부터 시작하는 딥러닝
- 파이썬 pandas
- Django
- 텍스트 분류
- 구글 BERT의 정석
- 가설검정
- 은준아 화이팅
- word2vec
- rnn
- 기술통계학
- Pandas
- 차원축소
- 회귀분석
- 코사인 유사도
- 감성분석
- 기초통계
- 다층 퍼셉트론
- F분포
- Today
- Total
데이터 한 그릇
기초통계5 : 확률의 이해 본문
- 사건에 확률을 부여하는 방법
- 결합확률, 한계확률, 조건부 확률
- 확률법칙과 확률나무
- 베이즈의 법칙
- 베이즈 법칙의 공식
https://kurt7191.tistory.com/9
기초통계4 : 수치를 이용한 기술통계학 기법 (ⅱ)
선형관계의 척도 최소자승법과 손익분기분석 그래프 기법과 수치 기법의 비교 https://kurt7191.tistory.com/8?category=1000998 기초통계4 : 수치를 이용한 기술통계학 기법 중심위치의 척도 변동성의 척도
kurt7191.tistory.com
들어가면서
지금가지 블로그의 ~기초통계4 까지는 기초통계의 두 가지 기법(그래프, 수치)에 대해서 살펴보았다. 이번 장부터는 추론통계학을 위한 확률에 대해서 다뤄볼 예정이다. 통계학의 주제가 어느정도 전환이 되었다는 점에 주목하면 좋을 것 같다.
사건에 확률을 부여하는 방법
확률을 소개하기 위해서는 먼저 확률실험(random experiment)에 대해서 살펴봐야한다. 책에 의하면 확률실험은 여러 가지 가능한 결과들 중 하나의 결과를 발생기키는 활동 또는 과정이다. 동전 던지기를 확률실험의 예로 들어보겠다. 동전을 던지면 나오는 결과는 앞면과 뒷면이다. 이 두 가지의 가능한 결과 중 앞면이 나오게 하는 활동, 뒷면이 나오게 하는 활동을 확률실험이라고 할 수 있다.
1)표본공간
확률을 부여하기 위해서는 두 가지 조건이 필요하다. 첫 번째로는 가능한 결과들을 모두 나열하는 것이다. 이를 완전(exhaustive) 하다고 한다. 두 번째로, 그 결과들은 상호배타적(mutually exclusive) 이어야 한다. 이렇게 완전하고 상호배타적인 결과들을 나열한 것을 표본공간(sample space) 이라고 부른다. 표본공간이란 확률실험으로부터 발생할 수 있는 모든 가능한 결과들을 나열한 것을 의미하며 이 결과들은 앞서 말했듯이 완전해야하며 상호배타적이여야 한다.
이렇듯 표본공간이 준비가 되면 확률을 부여할 수 있게 된다. 여기서 부여되는 확률은 다음과 같은 두 가지의 조건을 만족시켜야만 한다.
1. 어느 한 결과의 확률은 0과 1사이의 값을 가진다.
2. 표본공간에 있는 모든 결과에 대한 확률들의 합은 1이어야 한다.
표본공간의 모든 가능한 결과들에 확률을 부여하게 되면 위의 두 가지 조건을 만족시켜야만 한다. 그렇다면 표본공간의 각 결과에 대해서 확률을 부여하는 세 가지 방법에 대해서 살펴보자
2)확률을 부여하는 세 가지 방법
확률을 부여하는 세 가지 방법으로는 고전적 방법(classical approach)과 상대도수 방법(relative frequency approach), 주관적 방법(subjective approach) 이 존재한다. 고전적 방법의 예시로는 주사위의 확률과 동전 던지기의 확률을 예시로 들 수 있다. 상대도수는 한 결과가 발생하는 장기적 상대도수를 확률로 정의한다. 예를 들어서 2020년 통계학 수업의 A+ 성적을 받은 학생이 100명 중에 20 명이였다면 a+ 를 받은 학생의 상대도수는 20 / 100 일 것이다. 이를 확률의 추정치로 사용한 것이 상대도수 방법이라고 할 수 있다. 마지막으로는 주관적 방법이다. 주관적 방법은 한 사건의 발생에 대하여 가지고 있는 확신의 정도를 확률로 칭한 것을 말한다.
3)사건의 정의와 확률
표본공간을 구성하고 있는 가능한 결과들 중 하나를 단순사건(simple event) 이라고 칭한다. 모든 사건들은 표본공간에 있는 하나 이상의 단순사건들로 구성이 된다. 즉, 단순사건은 사건의 요소이다. 결국 사건(event)은 하나의 단순사건이거나 둘 이상의 단순사건을 칭한다.
그렇다면 사건의 확률은 어떻게 정하는지 살펴보자. 어떤 한 수업에서 받을 수 있는 점수는 A B C D F 라고 가정해보자. 여기서 표본공간은 A B C D F 라고 할 수 있다. 표본공간의 단순사건에 확률을 부여하는 방법은 앞서 세 가지임을 살펴보았다. 이 중에서 상대도수 방법을 사용하여 각각의 단순사건에 확률을 부여했다고 가정해보자.
P(A) = 0.20
P(B) = 0.30
P(C) = 0.25
P(D) = 0.15
P(F) = 0.10
여기서 과목을 통과하는 것은 A학점부터 D학점까지라고 가정해보자. 그렇다면 이 과목을 통과할 확률은 F일 때의 단순사건을 제외한 나머지 사건들의 확률의 합이라고 할 수 있다. 따라서 이 과목을 통과할 확률은 0.90 이라고 할 수 있다.
결합확률, 한계확률, 조건부확률
이절에서는 관련된 사건들의 확률로부터 더 복잡한 사건의 확률을 계산하는 방법에 대해서 다루겠다. 예를 들어서 두 개의 주사위를 던졌을 때 두 개의 주사위 숫자의 조합의 확률을 구하려고 할 경우 더 복잡한 사건의 확률을 구해야만 한다.
1)교사건과 결합확률
만일 사건 A와 사건 B가 동시에 일어난다면 이를 교사건(intersection) 이라고 칭한다. 이 교사건의 확률을 결합확률(joint prob-ability) 라고 칭한다.
2)한계확률
한계확률을 이해하기 위해서 하나의 표를 가정해보자.
| 뮤추얼 펀드의 수익률이 시장수익률보다 높음 | 뮤추얼 펀드의 수익률이 시장수익률보다 높지 않음 | |
| 상위 20위 대학의 MBA 학위 취득 | 0.11 | 0.29 |
| 상위 20위 이외 대학의 MBA 학위 취득 | 0.06 | 0.54 |
한계확률(marginal probability) 은 이름 그대로 위의 표에서 각 행의 확률의 합과 각 열의 확률의 합을 더한 것을 의미한다. 예를 들어서 상위 20위 대학의 MBA 학위를 취득한 사람이 뮤추얼 펀드의 수익률이 시장수익률보다 높을 확률과 상위 20위 대학의 MBA 학위 취득한 사람이 뮤추얼 펀드의 수익률이 시장수익률보다 높지 않을 확률을 구한다면 0.40 이라는 확률을 기록할 것이다. 이러한 방식으로 한계확률을 구하게 되면 밑의 표와 같다.
| 뮤추얼 펀드의 수익률이 시장수익률보다 높음 | 뮤추얼 펀드의 수익률이 시장수익률보다 높지 않음 | 합계 | |
| 상위 20위 대학의 MBA 학위 취득 | P(A1 and B1) = 0.11 | P(A1 and B1) = 0.29 | P(A1) = 0.40 |
| 상위 20위 이외 대학의 MBA 학위 취득 | P(A2 and B1) = 0.06 | P(A2 and B2) = 0.54 | P(A2) = 0.60 |
| 합계 | P(B1) = 0.17 | P(B2) = 0.83 | 1.00 |
3)조건부 확률
조건부 확률이란 어떤 조건이 주어졌을 때 어떤 사건이 일어날 확률을 의미한다. 기호로는 P(A|B) 라고 칭한다. 여기서 " | " 는 GIVEN 를 의미한다. 만일 위의 표를 예시로하여, 상위 20위 대학의 MBA 학위 취득자라는 조건하에서 뮤추얼 펀드의 수익률이 시작 수익률보다 높을 확률을 구한다고 해보자. 여기서 상위 20위 대학의 MBA 학위 취득의 확률을 구하면 0.11 + 0.29 로 0.40 이라고 할 수 있다. 즉, 만일 100명의 사람이 있을 때 40명은 상위 20위 대학의 MBA 학위 취득자라는 이야기다. 그 중에 우리가 구하려고 하는 확률은 뮤추얼 펀드의 수익률이 시장 수익률보다 높을 확률이니 11 / 40 라고 할 수 있으며 이 수치가 조건부 확률의 확률이라고 할 수 있다. 정리하자면 다음과 같다.
조건부 확률
사건 B가 발생한 후 사건 A가 발생할 확률은 다음과 같다.
P(A|B) = P(A and B) / P(B)
사건 A가 발생한 후 사건 B가 발생할 확률은 다음과 같다.
P(B|A) = P(A and B) / P(A)
4)독립사건과 합사건
조건부 확률을 계산하는 목적 중 하나는 두 사건이 관련되어 있느냐를 결정하는 것이다. 만일 P(A|B) = P(A) 이거나 P(B|A) = P(B) 이면 A와 B는 서로 독립이라고 할 수 있다. 합사건이란 두 사건 중 적어도 하나의 사건이 일어날 확률을 의미한다. A or B 로 표시된다.
확률법칙과 확률나무
1)여사건법칙
만일 사건 A의 여사건이라고 한다면 사건 A가 일어나지 않을 확률이라고 할 수 있다.
1 - P(A)
2)곱셈법칙
곱셈법칙은 두 사건의 결합확률(A and B) 을 계산하기 위해 사용된다. 앞서 조건부 확률의 법칙은 P(A|B) = P(A and B) / P(B) 임을 살펴보았다. 이 공식을 그대로 활용한다면 아래와 같은 공식이 나온다.
P(A and B) = P(A|B)P(B)
3)덧셈법칙
덧셈법칙은 두 사건의 합사건 확률을 계산할 수 있게 해준다. 밑의 공식이 덧셈법칙이라고 할 수 있다.
P(A and B) = P(A) + P(B) - P(A and B)
4)확률나무
앞서 배운 세 개의 확률법칙을 잘 활용하기 위한 방법은 확률나무(probability tree)를 사용하는 것이다. 확률나무는 직접 그림을 보고 이해하는 것이 빠르다. 밑의 그림은 확률나무이다.
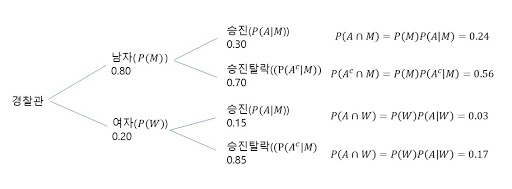
경찰관 직원의 성별 승진 여부에 관련된 확률을 구한다고 가정해보자. 그림상에 보이는 바와 같이 남자를 뽑는 확률은 P(M) 이라고 할 수 있다. 따라서 여자를 뽑을 확률은 1 - P(M) 이라고 할 수 있다. 그 이후에는 각각의 남녀 항목에 따라서 조건부확률이 적용이 된다. 경찰관이 남자인 조건하에서 승진할 확률은 조건부확률로 P(A|M) 이라고 할 수 있다. 반대로 승진탈락할 확률은 P(-A|M) 라고 할 수 있다. 여자또한 마찬가지로 P(A|W), P(-A|W) 라고 할 수 있다. 마지막 남자이면서 승진할 결합확률은 이 두 가지의 확률을 곱하면서 구할 수 있다. 즉, P(M) X P(A|M) 이라고 할 수 있다. 이 확률에 대한 해석을 확실히 하는 것이 중요하다. 이 확률은 남자이면 승진할 확률이 아니라 무작위로 경찰관 한명을 뽑았는데 남자이면서 승진한 사람일 확률을 의미한다.
베이즈의 법칙
조건부 확률은 어떤 하나의 사건이 원인으로 발생할 때 다른 어떤 특정 사건이 일어날 확률에 관한 확률이다. 그러나 어떤 결과 사건을 목격하고 그 결과 사건의 원인이 되는 사건이 발생할 확률에 대해서 구하고 싶을 수 있다. 이 때 사용되는 것이 베이즈의 법칙(Bayes's Law) 이다.
책의 예제 하나를 통해서 베이즈의 법칙을 이해해보도록 하자. 예제는" MBA 지원자는 GMAT 준비과목을 수강하여야 하는지" 에 관한 것이다. GMAT시험은 MBA 프로그램의 모든 지원자들이 치루어야 하는 필수시험이다. 만일 GMAT 시험을 합격하지 못한다면 MBA 를 졸업할 수 없다. GMAT 시험의 합격 기준은 650점 이상이다. 이런 규칙 때문에 학생들의 GMAT 시험 통과를 돕기위한 준비과목들이 존재한다. GMAT 시험을 치룬 학생들의 점수를 서베이 해본 결과 650점 이상의 점수를 취득한 사람들 중에서 52%는 준비과목을 들은 반면에 650점 미만의 GMAT 점수를 취득한 사람들 중에서 23% 만이 GMAT 준비과목을 수강하였다.
어떤 사람이 자신의 GMAT 시험을 통과할 확률을 10%라고 생각하고 있다. 확률이 낮다고 생각한 그는 시험을 통과하기 위해서 준비과목을 수강할 생각을 하고 있다. 만일 650점 이상의 점수를 취득할 확률이 두 배 이상 되게 된다면 그는 기꺼이 준비과목을 수강할 생각이다. 그는 어떻게 해야할까?
이 문제를 해결하기 위해서 몇 가지 조건을 가정하자. 먼저 확률을 구하기 위한 변수들을 선언하자.
A = GMAT 점수가 650점 이상이다.
-A = GMAT 점수가 650점 미만이다.
B = 준비과목들을 수강한다.
-B = 준비과목들을 수강하지 않는다.
다음으로는 각각의 변수의 확률을 구해보자. 앞서 학생은 자신이 GMAT 시험을 통과할 확률을 10% 라고 생각했다. 따라서 P(A) = 0.10 이라고 할 수 있다. 따라서 P(-A) = 0.90 이다. 또한 위에서 합격한 사람들 중에서 52%가 준비과목들을 들었다고 했으니 P(B|A) = 0.52 이다. 따라서 여사건법칙에 의해서 P(-B|A) 는 0.48 이다. 또한 불합격한 사람들 중에서 23%가 준비과목들을 듣었기 때문에 P(B|-A) = 0.23 이다. 여사건법칙에 의해서 P(-B|-A) = 0.77 이다. 확률과 조건부 확률을 정리해보자면 아래와 같다.
P(A) = 0.10
P(-A) = 0.90
P(B|A) = 0.52
P(-B|A) = 0.48
P(B|-A) = 0.23
P(-B|-A) = 0.77
우리가 구하고 싶은 확률은 그가 준비과목들을 들었을 때 합격할 확률이다. 따라서 P(A|B) 이다. 앞서 조건부확률들이 합격한 사람이면 수강과목을 들었을 확률이라고 한다면 베이즈 정리는 그 반대라고 할 수 있다. P(A|B) = P(A and B)/P(B) 라고 할 수 있다. 이 때 우리는 분모와 분자의 확률을 단 한 개도 알고있지 못하다. 이럴 때 유용하게 사용할 수 있는 방법론이 확률나무라고 할 수 있다.
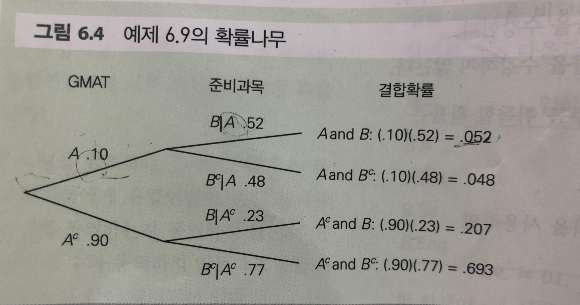
앞서 확률나무를 통해서 조건부서식과 결합확률의 차이를 인식해야함을 살펴보았다. 따라서 A and B의 해석은 조건부확률의 해석과 달리 어떤 학생을 뽑았을 때 그 사람이 GMAT 시험을 통과했으면서 준비과목을 들었던 학생일 확률을 의미한다. 이 확률을 구하기 위해서는 위의 사진과 같아. P(A) X P(B|A) 를 해야만 한다. 이를 통해서 0.10 X 0.52 를 곱하면 0.052 의 확률이 도출된다. 즉, P(A and B) = 0.52 이다. 마지막으로 분모의 P(B) 의 확률을 구할일만 남았다. P(B) 의 확률은 B일 모든 확률을 더하면 된다. 즉, A 그리고 B일 확률 -A 이면서 B일 확률을 더하면 B의 확률이 도출된다. 위의 그림을 보면 이해하기 더 편하다. 따라서 P(B) = 0.052 + 0.207 = 0.259 이다.
따라서 앞의 P(A|B) 의 확률은 0.052 / 0.259 = 0.201 이다. 따라서 준비과목을 듣고 GMAT 시험을 통과할 확률은 기존의 P(A) 일 확률인 0.10 의 두 배 이상이다. 따라서 그 사람은 준비과목을 수강신청 할 것이다.
베이즈의 정리로 이 예제를 해석한다면 P(A) 와 P(-A) 는 수강에 관한 의사결정을 하기 전에 미리 정해진 확률이기 때문에 사전확률(prior probability) 이라고 불린다. 지금까지 활용한 조건부확률(GMAT 시험을 통과한 사람이 준비과목을 들을 확률, p(b|a))은 우도확률(likelihood probability) 로 불린다. 마지막으로 우리가 구하려고 했던 P(A|B) 와 같은 조건부 확률은 사후확률(posterior probability) 또는 수정확률(revised probability) 이라고 불린다.
베이즈 법칙의 공식
베이즈 법칙의 공식은 확률나무보다 수식을 더 선호하는 사람들을 위한 법칙이라고 할 수 있다. 사건 B는 주어진 사건이고 A1 ~ Ak 까지도 사전확률이다. 우도확률은 P(B|A1) ~ P(B|Ak) 이다. 우리가 구하려고 하는 확률은 사후확률로 P(A1|B) ~ P(Ak|B) 이다. 베이즈 법칙은 다음 그림과 같다. 시간이 나면 의료검사와 건강보험 분야의 베이즈 통계학을 응용하는 문제도 다뤄보도록 하겠다.

정리
지금까지 확률과 통계에 대해서 살펴보았다. 크게 표본공간에 대해서 먼저 살펴보았으며 표본공간의 단순사건들의 조합이 사건임을 살펴보았다. 이 사건에 확률을 부여하는 방식이 세 가지 존재함을 살펴보았으며 그 중에 상대도수 방법을 가장 많이 사용함을 살펴보았다. 다음으로 확률의 종류가 결합확률, 한계확률, 조건부확률임을 살펴보았으며 확률의 법칙으로는 여사건법칙, 곱셈법칙, 덧셈법칙이 있음을 살펴보았다. 그리고 확률 법칙들을 잘 사용할 수 있는 방법인 확률나무를 살펴보았으며 조건부법칙의 반대라고 할 수 있는 베이즈정리에 대해서 gmat 시험의 예시를 통해서 살펴보았다. 마지막으로는 베이즈 정리 공식에 대해서 살펴보았다. 다음 장에서는 확률변수와 이산확률분포에 대해서 살펴보도록 하겠다.
'통계 > 기초통계' 카테고리의 다른 글
| 기초통계7 : 연속확률분포 (0) | 2021.03.07 |
|---|---|
| 기초통계6 : 확률변수와 이산확률분포 (0) | 2021.03.07 |
| 기초통계4 : 수치를 이용한 기술통계학 기법 (ⅱ) (0) | 2021.03.01 |
| 기초통계4 : 수치를 이용한 기술통계학 기법 (0) | 2021.02.28 |
| 기초통계3 : 그래프와 표를 이용한 기술통계학 기법 (ⅱ- 1) (0) | 2021.02.28 |

