Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- 가설검정
- 모두의 딥러닝
- F분포
- 밑바닥부터 시작하는 딥러닝
- 기술통계학
- Pandas
- 밑바닥부터 시작하는 딥러닝2
- 자연어 처리
- 구글 BERT의 정석
- numpy
- word2vec
- Django
- 머신러닝
- rnn
- 결정계수
- 회귀분석
- 코사인 유사도
- 다층 퍼셉트론
- 텍스트 분류
- 기초통계
- 최소자승법
- 은준아 화이팅
- student t분포
- 감성분석
- 오래간만에 글쓰네
- 군집화
- 차원축소
- 히스토그램
- 파이썬 pandas
- 텐서플로2와 머신러닝으로 시작하는 자연어처리
Archives
- Today
- Total
데이터 한 그릇
4)시계열의 탐색적 자료 분석3 본문
1. 유용한 시각화
시계열의 완벽한 탐색적 분석의 핵심을 그래프다
시간축에 대한 그래프를 반드시 시각화 해야만 한다
이 책의 저자는 복잡도에 따라서 다양한 시각화 기법을 살펴본다
1.1 1차원 시각화
require(timevis)
donations <- fread("donations.csv")
d <- donations[,.(min(timestamp), max(timestamp)), user]
names(d) <- c('content', 'start','end')
d <- d[start != end]
timevis(d[sample(1:nrow(d), 20)])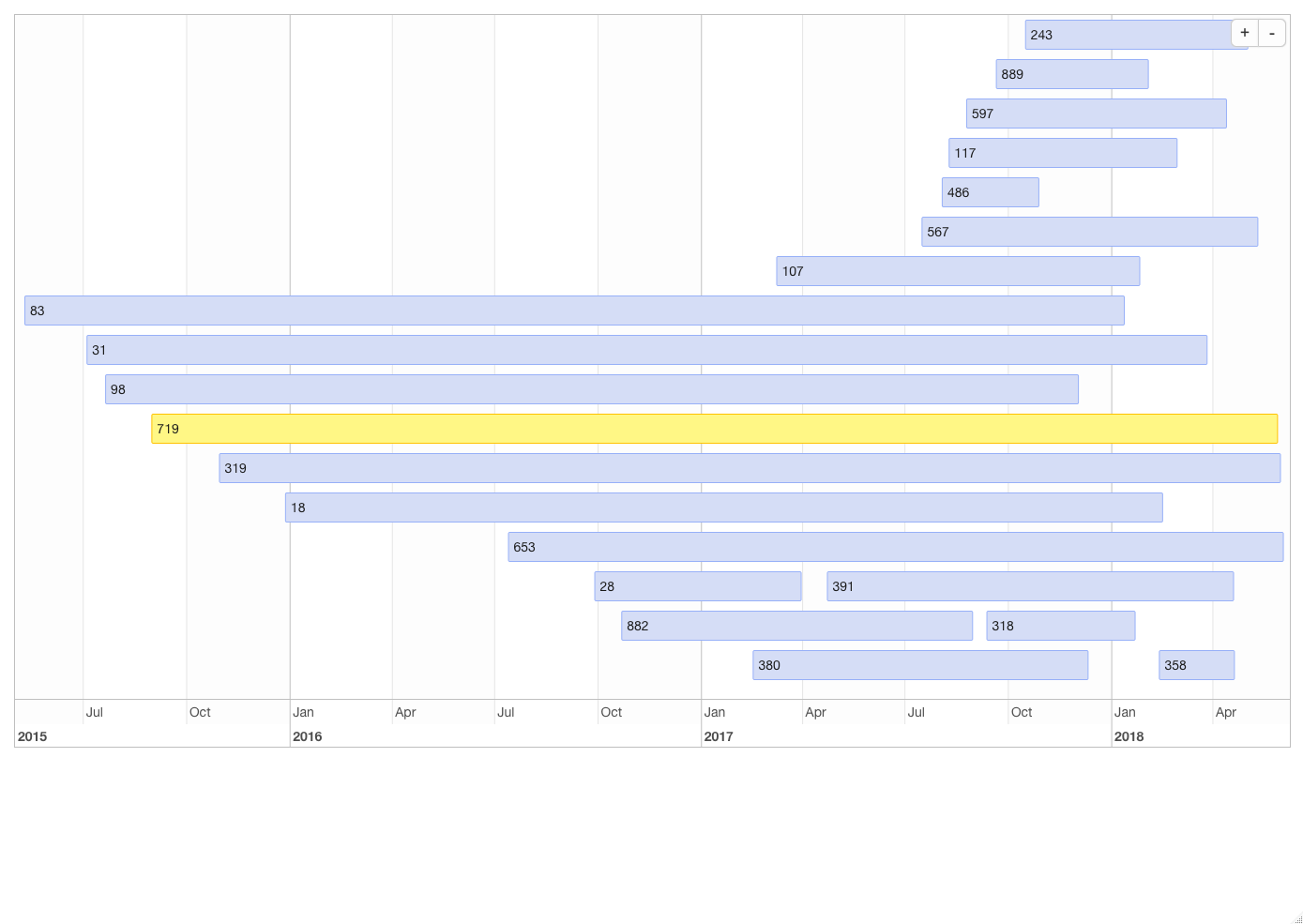
1.2 2차원 시각화
ts(matrix(AirPassengers, nrow = 12, ncol = 12))
AirPassenger 데이터를 사용하여 계절성과 추세를 살펴볼 예정
이때 시간이 선형적이라고 생각해서는 안된다. 시간이 한 개 이상의 축에서 나타나는 특별한 경우이다
매일, 매년 앞으로 나아가는 시간축은 당연히 있다. 추가로 시간, 요일 등에 따라서 시간을 펼쳐볼 수 있다.
이런 방법을 사용하면 특정 시간과 달에 특정 행동이 일어나는 계절성을 보다 쉽게 이해할 수 있다
단순한 선형적인 행동보다는 계절적인 행동 방식이 바로 시간의 시각화를 통해서 알고 싶은 부분
colors <- c('green','red','pink','blue',
'yellow','lightsalmon','black','gray',
'cyan','lightblue','maroon','purple')
matplot(matrix(AirPassengers, nrow = 12, ncol = 12),
type = 'l',col = colors, lty = 1, lwd = 2.5,
xaxt = 'n', ylab = 'Passenger Count')
legend("topleft", legend = 1949:1960, lty = 1, lwd = 2.5, col = colors)
axis(1, at = 1:12, labels = c("Jan", 'Feb','Mar','Apr',
'May',"Jun","Jul","Aug",
"Sep","Oct","Nov","Dec"))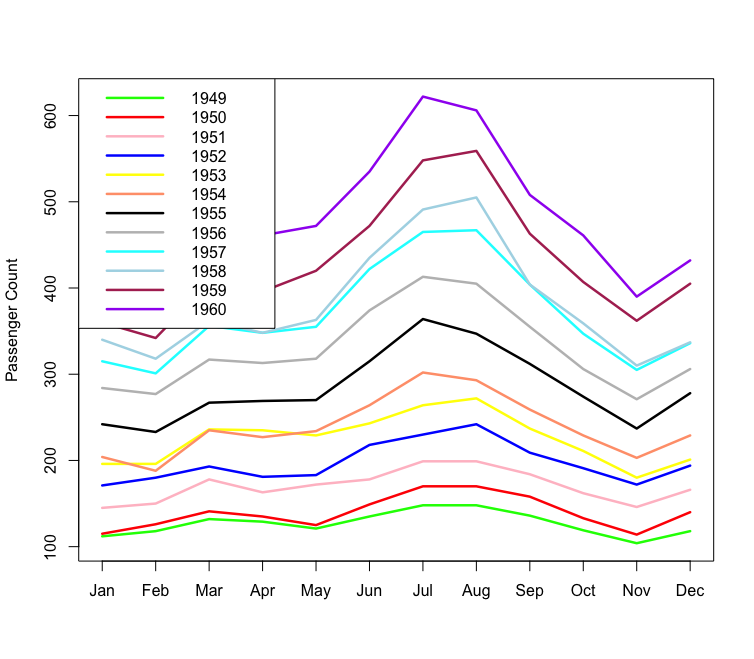
년도별 월별 시계열 데이터 변화 추이를 확인할 수 있다
R에서 제공하는 forecast 함수를 사용하면 쉽게 동일한 그림을 그릴 수 있다
require(forecast)
seasonplot(AirPassengers)
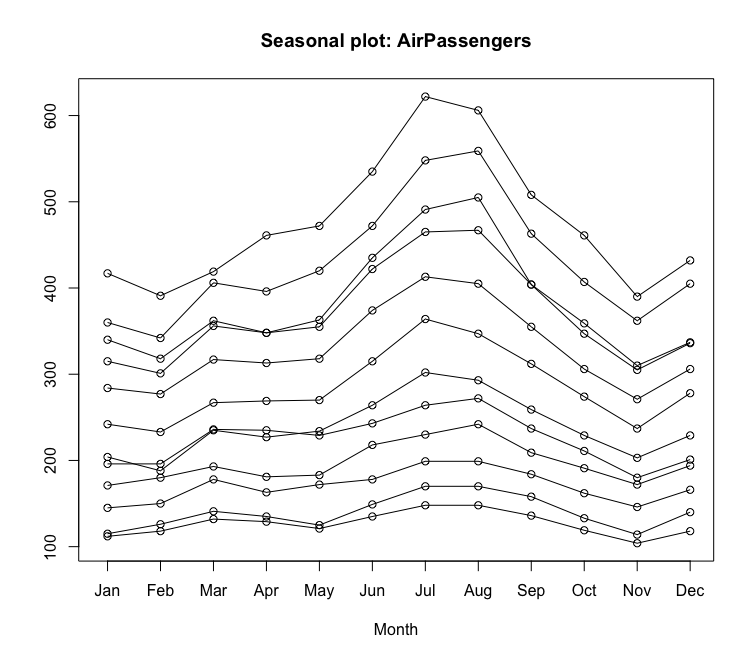
추가로 연도별 월별 곡선의 도표는 덜 표준적이지만 여전히 유용하다
months <- c("Jan","Feb","Mar","Apr","May","Jun",
"Jul","Aug","Sep","Oct","Nov","Dec")
matplot(t(matrix(AirPassengers, nrow = 12, ncol = 12)),
type = 'l', col = colors, lty = 1, lwd = 2.5)
legend("left",legend = months, col = colors, lty = 1, lwd = 2.5)
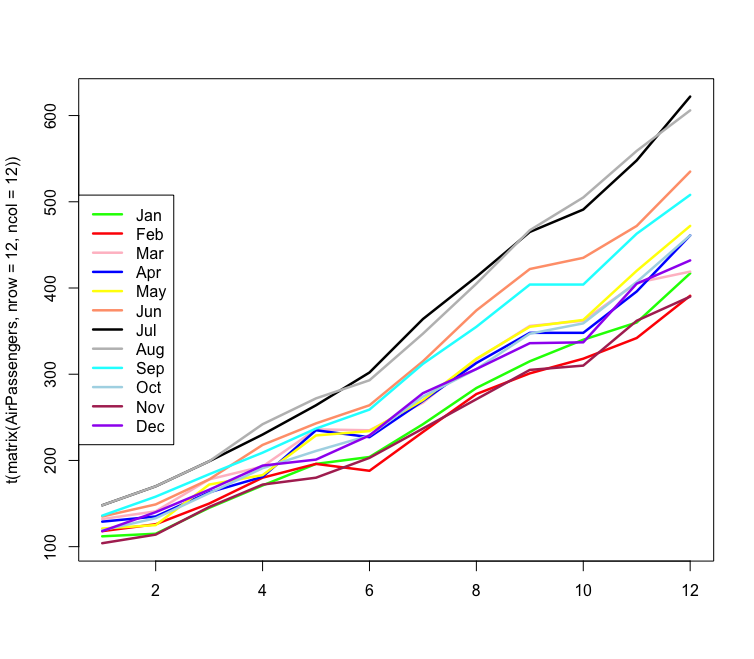
forecast 패키지를 통해 유사한 그림을 그릴 수 있다
monthplot(AirPassengers)
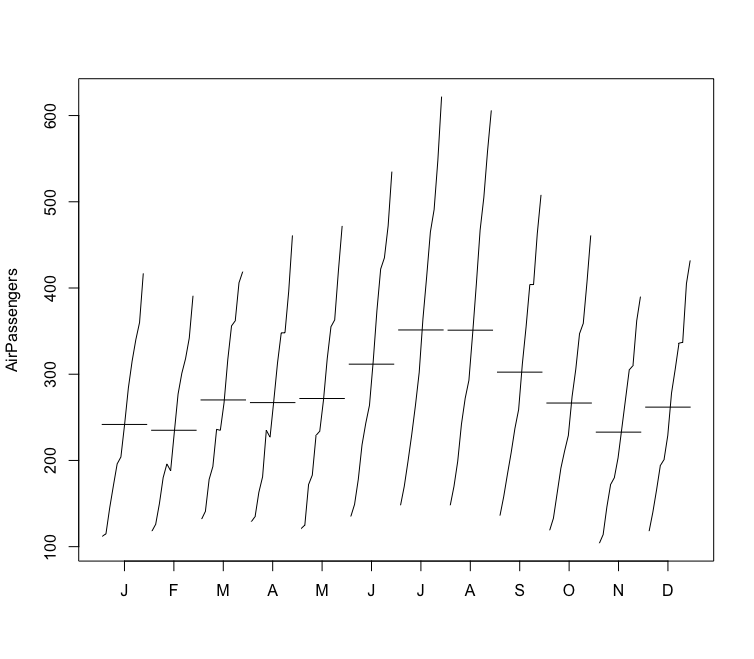
- 시계열에는 그리고자 하는 도표에 대해 하나 이상의 유용한 시간축이 있다, 데이터셋의(1~12월)과 연도(1949 ~ 1960년) 축 두 개를 사용했다
- 선형적으로 도표를 그린 것에 비해 시계열 데이터를 누적시킨 시각화는 많은 유용한 정보와 예측의 세부 사항을 얻게 해준다
시계열 데이터에서 한 축은 시간, 다른 한 축은 관심 단위로 구성된 2차원 히스토그램을 생각해볼 수 있다
hist2d <- function(data, nbins.y, xlabels){
##최댓값과 최솟값을 포함하는 균등한 크기의 ybins를 만든다
ymin = min(data)
ymax = max(data) * 1.0001
##포함/불포함의 걱정을 피하기 위한 게으른 방법
ybins = seq(from=ymin, to=ymax, length.out = nbins.y+1)
#적절한 크기의 제로 행렬을 만든다
hist.matrix=matrix(0,nrow=nbins.y, ncol = ncol(data))
#행렬의 각 행은 하나의 데이터 점을 표현한다
for(i in 1:nrow(data)){
ts = findInterval(data[i,], ybins)
for(j in 1:ncol(data)){
hist.matrix[ts[j],j] = hist.matrix[ts[j],j] +1 > hist.matrix
}
}
hist.matrix
}
h = hist2d(t(matrix(AirPassengers, nrow = 12, ncol = 12)),5, months)
image(1:ncol(h), 1:nrow(h), t(h), col = heat.colors(5),
axes = FALSE, xlab = 'Time', ylab = 'Passenger Count')
이외에 여러 가지 방법이 나오는데 교재 154pg 부터 참조
- 다음 장은 시계열 데이터의 시뮬레이션 파트인데, 다른 시계열 토픽이 더 중요하다고 생각하기 때문에 마지막에 공부하는걸로 남겨둔다
- 그 다음 파트는 시계열 데이터 엔지니어에 관련된 시간 데이터 저장이다
- 이땐, 엔지니어 관련 지식보단 현재 분석 지식이 더 급하기 때문에 그 다음 장으로 넘어갈 예정이며 이 또한 다른 파트 학습을 끝낸 이후에 시도할 예정
따라서 다음 파트는 시계열의 통게 모델을 살펴볼 것
'시계열 분석 > Practical TIme Series Analysis' 카테고리의 다른 글
| 5)시계열의 통계 모델 (0) | 2022.10.25 |
|---|---|
| 번외)딥러닝을 이용한 시계열 예측 (0) | 2022.10.14 |
| 4)시계열의 탐색적 자료 분석2 (0) | 2022.10.13 |
| 4)시계열의 탐색적 자료 분석 (0) | 2022.10.12 |
| 3)계절성 데이터, 시간대, 사전관찰의 방지 (0) | 2022.10.12 |
Comments



