| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 기술통계학
- 텍스트 분류
- Pandas
- 은준아 화이팅
- 최소자승법
- 코사인 유사도
- 텐서플로2와 머신러닝으로 시작하는 자연어처리
- 히스토그램
- word2vec
- 감성분석
- Django
- 머신러닝
- 차원축소
- 군집화
- 모두의 딥러닝
- F분포
- student t분포
- 기초통계
- 오래간만에 글쓰네
- 다층 퍼셉트론
- 구글 BERT의 정석
- 파이썬 pandas
- numpy
- 밑바닥부터 시작하는 딥러닝2
- 결정계수
- 자연어 처리
- 밑바닥부터 시작하는 딥러닝
- 가설검정
- rnn
- 회귀분석
- Today
- Total
데이터 한 그릇
군집화) GMM(Gaussian Mixture Model) 본문
- GMM(Gaussian Mixture Model) 소개
- GMM과 K-평균 비교
GMM 소개
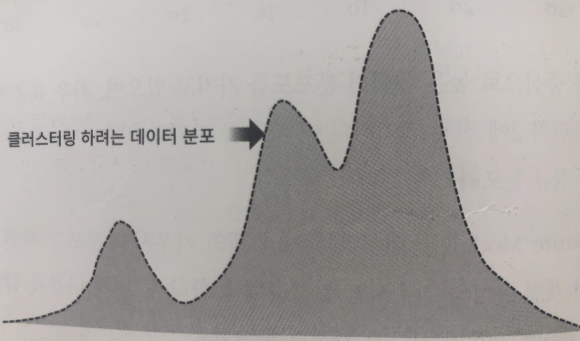
GMM은 분석 대상의 데이터 셋이 여러 개의 가우시안 분포를 가지고 있는 데이터들의 결합으로 생성됐다는 가정하에서 군집화를 수행하는 방식을 말한다. 만일 분석 데이터 셋이 세 개의 가우시안 분포가 합쳐져 있다고 가정해보자. GMM분석은 먼저 전체의 데이터 셋에서 개별 가우시안 분포를 추출한다.
만일 정규분포 여러개가 합쳐진 데이터 셋이라면 전체 데이터 셋의 분포모양을 통해서 그러한 사실을 쉽게 파악 가능하다.(분포의 모양 때문에) 만일 각각의 분포를 추출해서 분석을 하게 되면, 각각의 군집을 따로 분석한 것과 같다. 결국 GMM군집화 방식은 LABEL들이 추출된 각각의 분포 중에 어디에 속하는지 결정하는 방식이다.

from sklearn. datasets import load_iris
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
iris = load_iris()
feature_names = ['sepal_length','sepal_width','petal_length','petal_width']
iris_df = pd.DataFrame(data = iris.data, columns = feature_names)
iris_df['target'] = iris.target
앞서 처럼 군집화를 하기 위해서 아이리스 데이터를 데이터 프레임화 한다.
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components = 3, random_state = 0)
gmm.fit(iris.data)
gmm_cluster_labels = gmm.predict(iris.data)
iris_df['gmm_cluster'] = gmm_cluster_labels
iris_df['target'] = iris.target
iris_result = iris_df.groupby(['target'])['gmm_cluster'].value_counts()
print(iris_result)
sklearn.mixture에서 GaussianMixture를 import 한다. n_cluster가 아니라 n_components로 군집 개수를 설정한다. 그리고 예측한 결과를 gmm_cluster에 집어넣는다. 그 후 그룹화를 통해서 정확도를 확인한다.
GMM과 K-평균의 비교
k-means 같은 경우에는 데이터의 분포가 원형일 때 분석의 성능이 좋다. 만일 mark_blobs로 군집을 만들 때 표준편차를 작게 설정한다면, 데이터의 분포는 원형의 모습을 가지게 된다. 하지만 k-means는 데이터가 길쭉한 타원형으로 늘어선 경우에 군집화를 잘 수행하지 못한다.
from sklearn. datasets import make_blobs
X,y = make_blobs(n_samples = 300, n_features = 2, centers = 3, cluster_std = 0.5, random_state = 0)
transformation =[[0.60834549,-0.63667341],[-0.40887718,0.85253229]]
X_aniso = np.dot(X, transformation)
clusterDF = pd.DataFrame(data = X_aniso, columns =['ftr1','ftr2'])
clusterDF['target'] = y
visualize_cluster_plot(None,clusterDF, 'target', iscenter = False)
plt.savefig('cluster5')
군집화 데이터 셋을 make_blobs을 통해서 만들어 보고 이 데이터를 조작하기로 한다. make_blobs에서 샘플을 300개 피처를 2개로 설정을 하고 군집 중심점을 3개로 지정한다. 데이터의 분포는 원형이 아닐 경우에 kmeans의 성능이 떨어지는 것을 보이고 싶기 때문에 원형이 아닌 분포로 만든다.
우리가 만든 데이터 군집 세 개는 데이터의 분포가 원형이 아니다. 따라서, kmeans의 성능은 떨어지게 된다.
kmeans = KMeans(3, random_state = 3)
kmean_labels = kmeans.fit_predict(X_aniso)
clusterDF['kmeans_labels'] = kmean_labels
visualize_cluster_plot(kmeans, clusterDF, 'kmeans_labels',iscenter = True)
plt.savefig('cluster6')
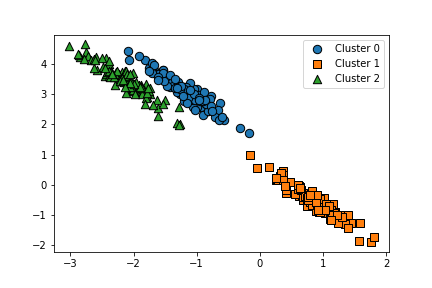
군집화 분류가 제대로 되지 않았음이 보인다.
gmm = GaussianMixture(n_components = 3, random_state = 0)
gmm_label = gmm.fit(X_aniso).predict(X_aniso)
clusterDF['gmm_label'] = gmm_label
visualize_cluster_plot(gmm, clusterDF, 'gmm_label', iscenter = False)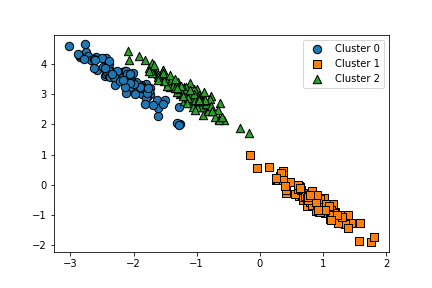
GMM분포, 가우시안 분포를 이용한 군집화를 통해서 분류가 잘 된 모습을 볼 수 있다.
=> 분포의 모양이 원형일 경우 K-MEANS 유용, 그 이외에 모양일 경우 GMM유용
'머신러닝 > 군집화' 카테고리의 다른 글
| Customer Personality Analysis (0) | 2021.12.08 |
|---|---|
| 군집화)평균 이동 (0) | 2021.05.26 |
| 군집화)DBSCAN 군집화 (0) | 2021.05.25 |
| 군집화 개요, k-평균 알고리즘 (0) | 2021.05.21 |



