| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- rnn
- 군집화
- 가설검정
- F분포
- 기초통계
- 차원축소
- numpy
- Django
- 감성분석
- 텍스트 분류
- word2vec
- 히스토그램
- 밑바닥부터 시작하는 딥러닝2
- student t분포
- Pandas
- 모두의 딥러닝
- 머신러닝
- 텐서플로2와 머신러닝으로 시작하는 자연어처리
- 밑바닥부터 시작하는 딥러닝
- 최소자승법
- 코사인 유사도
- 구글 BERT의 정석
- 기술통계학
- 결정계수
- 은준아 화이팅
- 오래간만에 글쓰네
- 자연어 처리
- 파이썬 pandas
- 다층 퍼셉트론
- 회귀분석
- Today
- Total
데이터 한 그릇
8)시계열을 위한 머신러닝 본문
시계열 분석에서의 머신러닝 기법은 비교적 새로운 분야이지만, 가능성을 보여준 분야다
우리가 지금까지 다뤘던 (AR, MA, ARMA, ARIMA) 에서 다뤘던 통계 모델과는 다르다
하지만 머신러닝이 다른 분야에서 유용했던것처럼 시계열에서도 유용함을 입증했다
시계열을 위한 머신러닝은 클러스터링과 트리 기반 방법론으로 예측과 분류 문제를 다룬다
시계열의 특징 생성은 트리 기반 방법론에서 반드시 필요한 과정이다
ARIMA 모델과는 달리 '시간을 인식' 하는 방법론이 아니기 때문이다
클러스터링 및 거리 기반의 분류는 입력(input) 으로 원본 시계열이나 특징을 사용할 수 있다
시계열 자체를 입력으로 사용하려면, 동적시간워핑(DTW) 라는 거리 평가 지표를 알아야 한다
시계열에 직접적으로 적용되는 동적시간워핑은 데이터 전체에 대한 시간 정보를 보존한다
제한된 특징 목록을 사용하는 방법과는 다르다
시계열 분류
이번 절은 원시 뇌전도(electroencephalogram(eeg)) 시계열 데이터에 대한 특징을 만드는 예를 다룬다
이렇게 만들어진 특징은 머신러닝 알고리즘에 사용된다
EEG 시계열의 특징을 추출한 다음 결정 트리(decision tree) 기법으로 EEG 데이터를 분류한다
특징의 선택과 생성
이전 장에서는 시계열 특징 생성의 목적에 대한 일반적인 내용을 다뤘다
또한 tstfesh 로 시계열을 위한 특징 생성의 간단한 예를 다뤘다
이번에는 cesium 이라는 또 다른 시계열 관련 패키지로 특징을 생성하는 방법을 배워보자
cesium 패키지의 한 가지 장점은 여러 가지 유용한 데이터셋을 제공한다는 점
여기에는 2001년 연구 논문에서 얻은 eeg 데이터셋도 포함한다
cesium 이 제공하는 편리한 함수를 사용해서 데이터셋을 다운로드한다
from cesium import datasets
eeg = datasets.fetch_andrzejak()
이 시계열들을 분류하기 위한 아이디어는 데이터의 일부 샘플을 확인하여 얻을 수 있다
import matplotlib.pyplot as plt
plt.figure(figsize = (10,7))
plt.subplot(3,1,1)
plt.plot(eeg['measurements'][0])
plt.legend(eeg['classes'][0])
plt.subplot(3,1,2)
plt.plot(eeg['measurements'][300])
plt.legend(eeg['classes'][300])
plt.subplot(3,1,3)
plt.plot(eeg['measurements'][450])
plt.legend(eeg['classes'][450])
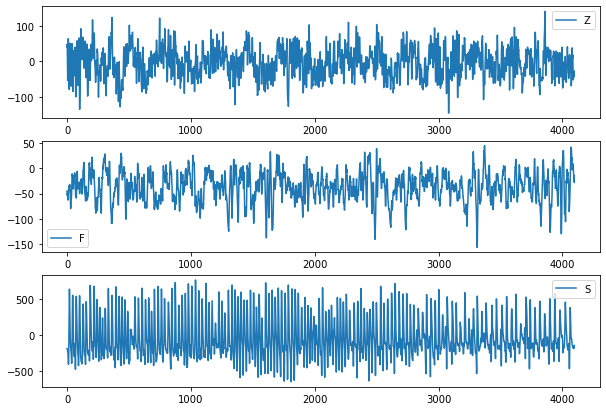
위의 그림에서 EEG 그래프가 현저히 다르다는 사실은 놀라울 일이 안디ㅏ
건강한 사람과 간질 환자를 대상으로 서로 다른 두뇌 활동을 측정한 것이기 때문이다
이 시각화는 특징 생성에 대한 가이드를 제공한다
가령 Z와 F는 S보다 덜 편향된 것으로 보이며 y축을 보면 각 범주는 꽤 다른 범위의 값으로 구성된 것을 알 수 있다
이러한 사실은 진폭이 유용할 수 있다는 것을 시사한다, 단지 전반적인 진폭뿐만 아니라, 세 가지 범주에서 서로 다른 특성을 지닌 것으로 보이는 데이터의 전반적인 분포도 유용하다
먼저 이런 특징을 생성하기 위한 코드를 알아보자
from cesium.featurize import featurize_time_series as ft
features_to_use = ['amplitude',
'percent_beyond_1_std',
'percent_close_to_median',
'skew',
'max_slope']
fset_cesium = ft(times = eeg['times'],
values = eeg['measurements'],
errors = None,
features_to_use = features_to_use,
scheduler = None)
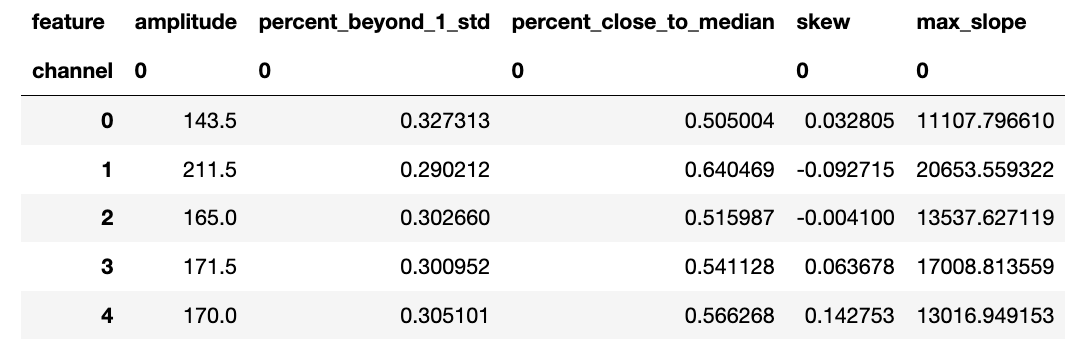
위의 코드를 실행하면 위와 같이 출력된다
이 값들 중 정규화되지 않은 값이 많다는 사실에 유의해야한다
일부 기법은 정규화된 입력을 가정하므로 주의하자
또한 각 특징이 나타내려는 것을 이해하고 우리가 이해한 바가 cesium 의 계산과 일치하는지도 확인해야 한다
오류 검사와 상식적인 확인의 한 예로, 시계열 샘플의 percent_beyod_1_std 를 확인할 수 있다
import numpy as np
np.std(eeg['measurements'][0])
np.mean(eeg['measurements'][0])
sample_ts = eeg["measurements"][0]
sz = len(sample_ts)
ll = -4.13 - 40.4
ul = -4.13 + 40.4
quals = [i for i in range(sz) if sample_ts[i] < ll or sample_ts[i] > ul]
len(quals)/sz #위의 특징결정 트리 기법
트리 기반 방법은 한 번에 한 단계씩, 비선형적인 방식으로 결정을 내리는 방식을 반영한다
가령 순서도처럼 한 번에, 한 단계씩 한 변수가 결정에 미치는 영향력을 생각하는 과정을 계속 반복하는 것이다
시계열 데이터 분석에서 사람의 행동이 결정 트리와 유사함을 보여주는 수많은 예가 있다
예를 들어 재량적 주식 투자자는 각 기술지표를 일련의 계층적 방식으로 사용할 가능성이 높다
먼저 한 기술지표에 따라 추세의 방향성에 대한 질문을 하고, 이어서 시간에 따른 변동성에 대한 질문을 하는 등 나무(트리)와 같은 구조가 된다
그러면 트리의 비선형성처럼 첫 번째와 두 번째 질문에 대한 답은 순차적으로 이루어져야 한다
이 거래자들의 머릿속에는 결정 트리와 같은 구조가 들어 있고,이 구조를 통해서 시장이 움직이는 방향을 예측한다
지금부터 다룰 예제는 EEG 데이터로부터 생성한 특징을 분류 작업에 활용 가능한 랜덤포레스트, 그레이디언트 부스팅 트리라는 두 가지 결정 트리 기법의 입력으로 사용한다. 이 예제의 작업 목표는 원시 데이터로 생성한 특징만으로 EEG 데이터를 분류하는 것
랜덤포레스트/그레이디언트 부스팅 트리
해당 이론적 내용은 아는 걸로 가정하고 생략
예제 코드
##python
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
fset_cesium.values, eeg['classes'], random_state = 21)
sklearn을 사용해서 데이터를 학습용과 테스트용 데이터셋으로 분리한다
from sklearn.ensemble import RandomForestClassifier
rf_clf = RandomForestClassifier(n_estimators = 10,
max_depth = 3,
random_state = 21)
rf_clf.fit(X_train, y_train)
먼저 랜덤포레스트부터 사용
EEG 데이터를 분류하는 모델을 쉽게 생성 가능
rf_clf.score(X_test, y_test) #0.616
결과를 확인해볼 결과 의학교육을 받지 않은 사람이 직접 분류하는 것보다는 더 나은 모델을 만들었다
다음으로 만들 Xgboost 도 간단하게 만들 수 있다
import xgboost as xgb
xgb_clf = xgb.XGBClassifier(n_estimators = 10,
max_depth = 3)
xgb_clf.fit(X_train, y_train)
xgb_clf.score(X_test, y_test)
이하 파라미터 값을 조정해서 모델의 성능들을 조정할 수 있다
코드 생략
분류와 회귀
앞선 예제에서는 시계열 분류에 랜덤포레스트와 그레이디언트 부스팅 트리를 사용하는 방법을 다뤘다
그런데 사실 시계열 예측에서도 이 두 방법론을 사용한다
여러 통계학자들은 예측에 있어서 머신러닝이 전통적인 통계 분석보다 덜 성공했다고 주장한다
하지만 그레이디언트 부스팅 트리가 등장한 이래로 지난 몇 년간의 결과로부터 큰 데이터가 주어질 때 머신러닝이 통계적인 모델의 성능을 앞지른 경우를 많이 볼 수 있다
그레이디언트 부스팅 트리 모델의 한 가지 장점은 자율적으로 접근하는 능력을 가졌다는 것
즉, 모델이 스스로 관련성이 적거나 노이즈가 많은 특징은 제거하고, 가장 중요한 특징들에 초점을 맞춘다는 것
그러나 이것만으로 최신 성능을 얻기에는 충분하지 않다
현재 모델을 향상하는 여러 가지 방법이 있다
XGBoost 의 옵션으로 생성 가능한 특징 중요도를 통해서 모델을 향상하기 위한 방향을 고민해볼 수 있다
이는 특징의 유용성을 파악하는 데 도움이 되고 이를 토대로 유용하다고 판단된 특징과 유사한 특징을 추가하는 방식으로 데이터셋을 확장할 수 있다
grid 서치 방식으로 모델의 파라미터를 조정해볼 수도 있다
그리고 원시 시계열의 잘못 레이블링된 데이터를 찾아보고 현재 모델에 사용된 특징으로 표현 가능한지를 확인하는 것도 도움이 된다
잘못 레이블링된 데이터를 보다 잘 묘사하는 특징을 추가하여 입력을 보강하는 방식을 고려해볼 수 있다
클러스터링
클러스터링의 기본 개념은 분석의 목적상 서로 유사한 데이터가 의미 있는 집단을 구성한다는 것
이러한 개념은 시계열 데이터뿐만 아니라 다른 데이터에도 적용
시계열에서의 클러스터링은 분류와 예측 모두에서 사용될 수 있다
클러스터링 알고리즘을 이용하면 원하는 수만큼의 집단을 모델의 학습 단계에서 식별할 수 있다
그리고 식별된 집단을 이용해 시계열의 범주를 규명하고 새로운 샘플이 소속될 집단을 인식할 수 있다
예측에서는 순수 클러스터링이나 거리 측정법을 이용하는 형태의 클러스터링이 사용될 수 있다
클러스터링과 관련 기법으로 미래의 수평성, h를 예측하는 몇 가지 옵션이 존재
이 경우 시계열 전체의 관측을 가지고 있는 게 아니라 N + h 번째의 시간 단계를 예측하기 위한 처음 N번의 단계에 대한 관측만을 가진 상황임을 유념
첫 번째 옵션:
특정 행동에 기반한 예측을 생성하기 위해서 그 행동을 규정하는 규칙을 사용하는 것
처음 N번의 시간 단계에 기반해 특정 시계열 샘플이 속한 클러스터를 결정, 해당 클러스터의 규칙에 따라 미래의 행동을 추론
구체적으로 해당 클러스터의 시계열값들이 시간 단계 N과 N+h 사이에서 변화하는 방식을 살펴보는 것
한편 사전관찰의 발생을 피하기 위해서 모든 시계열의 모든 부분이 아니라, 처음 N개의 단계에만 기반하여 클러스터링을 수행해야 한다
또 다른 옵션:
표본 시계열의 미래 행동을 표본 공간의 최근접이웃의 행동에 기반하여 예측하는 것
이런 시나리오에서는 처음 N개의 시간 단계에 대한 지표에 기반하여 해당 시계열의 최근접 이웃들을 찾고, 이 최근접 이웃들의 N+h 행동의 평균을 구한다. 그러면 현재 표본에 대한 예측을 얻게 된다
분류와 예측 두 분야 모두에서 시계열 간의 유사성을 평가하는 방법이 가장 중요한 고려 사항이다
클러스터링은 다양한 거리 지표로 수행될 수 있고, 고차원 문제의 거리 측정법 고안에 초점을 맞춘다
(ex. 두 지원자 두명 사이의 거리는? 두 개의 혈액 샘플 사이의 거리는?)
시계열 데이터에 클러스터링 기법을 적용하는 상황에서의 거리 측정법은 넓은 의미로 두 분류로 나뉜다
특징에 기반한 거리
시계열을 위한 특징을 생성, 이들을 데이터의 계산을 위한 좌표로 취급.
거리 측정 법의 선택 문제를 완전히 해결하지는 못하지만, 모든 비시계열 데이터셋이 거리 측정에 대해 제기한 수준으로 문제를 줄인다
원시 시계열 데이터에 기반한 거리
서로 다른 시계열이 얼마나 '가까운지' 를 결정하는 방법을 찾는다
가급적이면 서로 다른 시간의 규모, 서로 다른 측정 계수, 그 외 시계열 표본 사이의 있을 법한 불균형을 다룰 수 있는 방식이어야 한다
이제 두 가지 거리 측정법을 시계열 데이터셋에 적용할 예정
사용할 데이터셋의 각 샘플은 2d로 표현한 손글씨 단어 이미지를 1d시계열로 투영한 것
데이터에서 특징 생성하기
시계열 특징의 유사성에 기반하여 시계열 데이터셋 사이의 거리를 평가하는 방법을 살펴본다
이상적인 시나리오는 트리같은 기법을 사용하여 평가된 특징 중요도로, 중요하지 않거나 관심이 없는 시계열의 특징들을 미리 제거한 상황
이런 특징은 자칫 두 시계열의 차이를 잘못 나타내고 분류 및 예측 작업의 결과와 관련된 유사성을 나타내지 못할 수 이썽서 거리 측정에 포함하면 안된다
우리가 사용할 데이터는 FiftyWords 데이터 셋의 일부분
UEA 및 UCR 시계열 분류용 저장소에서 받을 수 있음
2003년에 작성된 역사적 문헌에 수기로 쓰여진 단어를 클러스터링하는 내용의 논문에서 공개된 것
이 논문의 저자는 2d 단어 이미지를 1d 곡선으로 매핑하는 방법을 사용해 단어의 윤곽을 개발했다
이 예제에선 투영 그래프 라는 단어가 등장하는데, 투영이란 2d 공간의 이미지를 1d 공간으로 변환한 것을 의미한다
순서가 중요한 1d 공간으로 표현된 데이터는 시계열 분석이 처리하기 좋은 형식이다
시간의 축이긴 하지만 실제로는 시간이 아니라 수기로 적힌 단어 데이터가 좌에서 우로, 차례대로 균등한 거리를 가지도록 나열되므로 그 개념은 같다, 따라서 시간 또는 시간적이라는 말이 가진 본래의 의미를 상황에 맞춰 자연스럽게 사용한다 (본 교재는)
투영한 이후에 살펴보면 고점들의 높이, 위치, 가파른 정도, 고점의 모영과 같은 특성을 고려해볼 수 있다
이때 설명하는 여러 특징이 시계열보다는 이미지 인식을 위한 특징인 것처럼 들릴지도 모르지만, 시각적 데이터는 시계열 데이터 대비 처리가 쉽고 보다 많은 직관을 얻을 수 있는 형식이다
이미지라는 측면에서 특징을 고민해보는 것은 도움이 되기도 하지만, 동시에 특징 생성이 어려운 이유를 설명해주기도 한다
데이터의 특징을 찾는 프로그래밍은 어려울 수 있다. (따라서 특징을 생성하기란 쉽지 않다)
또는 모든 범주별 데이터나 개별 데이터의 1D 히스토그램을 활용할 수도 있다. 이는 고점의 식별, 시계열의 전체 모양을 매핑하는 다른 대체 값을 찾는 데 계산적으로 덜 부담스러운 방법일 수 있다
plt.subplot(3, 2, 1)
plt.plot(words.iloc[1, 1:-1])
plt.title("Sample Projection Word " + str(words.word[1]), fontweight = 'bold', y = 0.8, fontsize = 14)
plt.subplot(3, 2, 2)
plt.hist(words.iloc[1, 1:-1], 10)
plt.title("Histogram of Projection Word " + str(words.word[1]), fontweight = 'bold', y = 0.8, fontsize = 14)
plt.subplot(3, 2, 3)
plt.plot(words.iloc[3, 1:-1])
plt.title("Sample Projection Word " + str(words.word[3]), fontweight = 'bold', y = 0.8, fontsize = 14)
plt.subplot(3, 2, 4)
plt.hist(words.iloc[3, 1:-1], 10)
plt.title("Histogram of Projection Word " + str(words.word[3]), fontweight = 'bold', y = 0.8, fontsize = 14)
plt.subplot(3, 2, 5)
plt.plot(words.iloc[5, 1:-1])
plt.title("Sample Projection Word " + str(words.word[11]), fontweight = 'bold', y = 0.8, fontsize = 14)
plt.subplot(3, 2, 6)
plt.hist(words.iloc[5, 1:-1], 10)
plt.title("Histogram of Projection Word " + str(words.word[11]), fontweight = 'bold', y = 0.8, fontsize = 14)
plt.suptitle("Sample word projections and histograms of the projections", fontsize = 18)
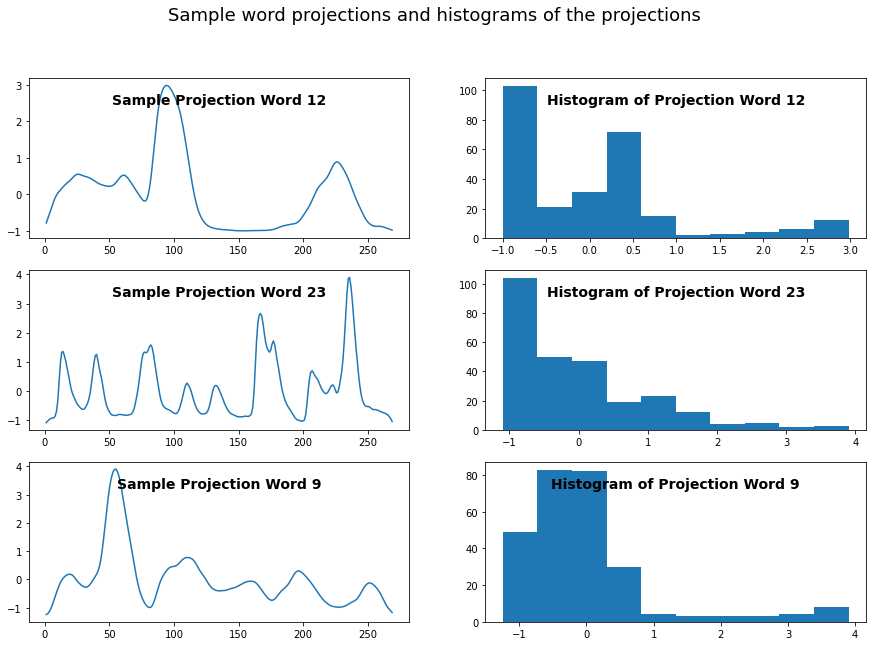
유용한 특징을 발견하기 위해 각 범주를 측정하는 또 다른 방법
특히 범주별 데이터의 히스토그램은 국소적 고점의 개수, 뒤틀림, 첨도와 같이 시계열 곡선을 잘 표현할 수 있는 대체 속성을 나타낸다
사람의 눈으로는 분명해 보이는 속성들은 코드로 표현하기 어렵다
상기 예시의 단어가 이상치가 아님을 확인
단어의 차이를 확인하는 두 단어에 대한 2D 히스토그램을 구성한다
## We can also consider the 2d histogram of a word
x = np.array([])
y = np.array([])
w = 23
selected_words = words[words.word == w]
selected_words.shape
for idx, row in selected_words.iterrows():
y = np.hstack([y, row[1:271]])
x = np.hstack([x, np.array(range(270))])
fig, ax = plt.subplots()
hist = ax.hist2d(x, y, bins = 50)
plt.xlabel("Time", fontsize = 18)
plt.ylabel("Value", fontsize = 18)
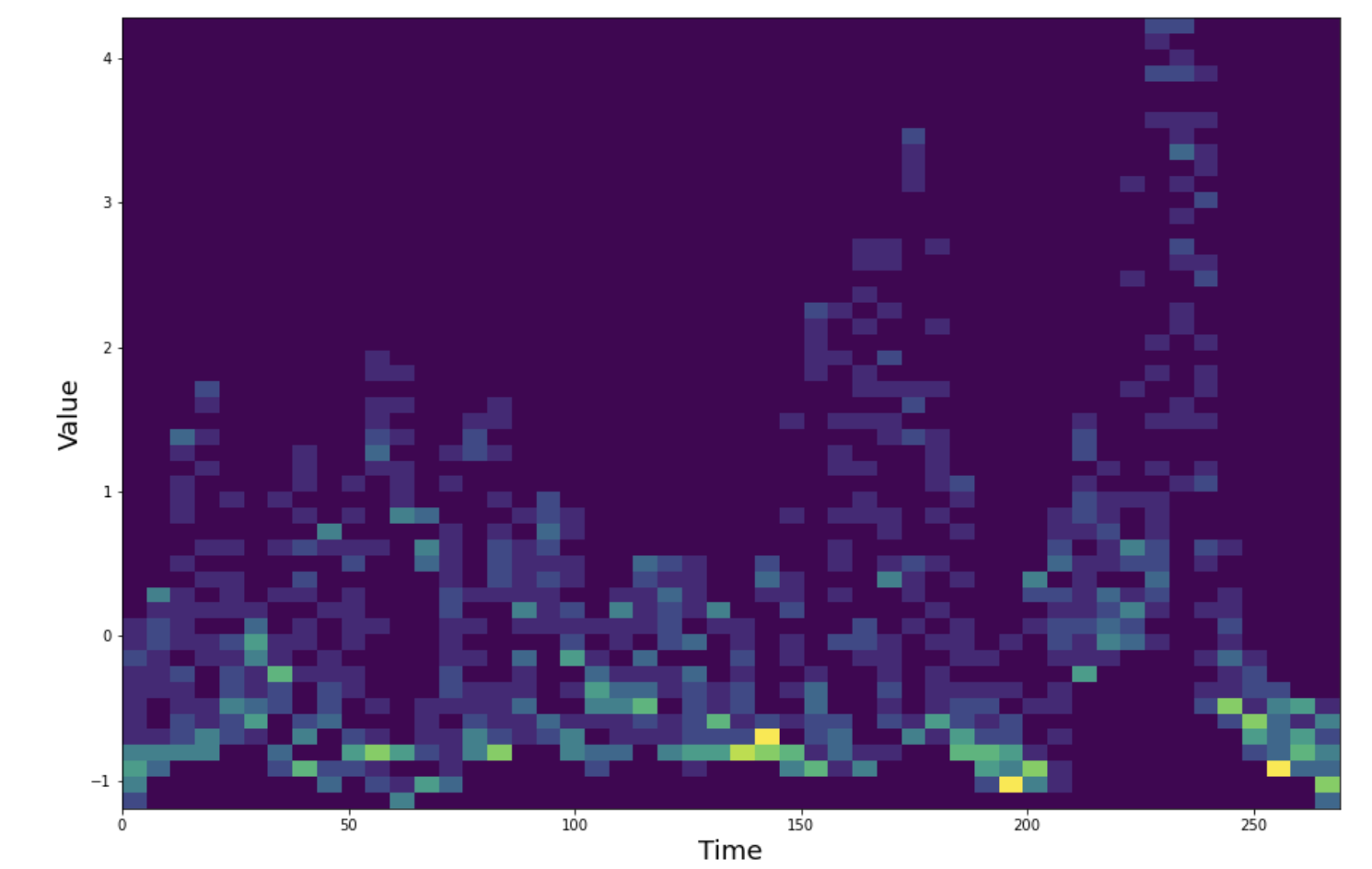
단어 word12를 1D 로 투영한 것에 대한 2D 히스토그램
x축은 투영된 각 시계열의 샘플/단어에 대한 시간 단계 270개
y축은 각 시간 단계에서의 측정값
위 그림은 데이터셋 중 word=12 에 포함된 모든 단어의 2D 히스토그램을 보여준다
또한 2D 히스토그램으로 이 범주 (12) 에 속한 최고점을 특정할 수 있다
2D 히스토그램은 개별 범주 내 특징에 대한 가변성을 알려주는 데 유용하여 하나의 데이터에 과도하게 의존하지 않는 특징의 구성 방식을 고려할 수 있다
생성하기 위한 특징들로는 단어 투영의 모양에서 파싱된 특징, 추가로 단어 투영 히스토그램의 모양에서 파생된 특징을 선택한다 (1D 요약을 또 다른 1D 요약으로 투영) 이는 2D 히스토그램에서 볼 수 있는 큰 '얼룩짐' 에 대한 대응으로, 고점은 있지만 그 위치가 안정적이지 않음을 표현한다
히스토그램을 사용해 생성한 각 단어 투영에 대한 이차적인 특징은 단순 단어 투영 자체보다 더 안정적이며 특성을 잘 나타낼 수도 있다
히스토그램은 값들의 위치를 틍징짓지 않고 그 값의 종류를 나타낸다
이는 고점이 안정적인 시간의 위치에 분포되지 않은 투영된 시계열을 다루는 본 예제에서 중요한 역할을 한다
words.shape
words_features = words.iloc[:, 1:271]
times = []
values = []
for idx, row in words_features.iterrows():
values.append(row.values)
times.append(np.array([i for i in range(row.values.shape[0])]))
from cesium import featurize
features_to_use = ["amplitude",
"percent_beyond_1_std",
"percent_close_to_median",
]
featurized_words = featurize.featurize_time_series(times=times,
values=values,
errors=None,
features_to_use=features_to_use,
scheduler = None)
featurized_words.to_csv('./featurized_words.csv')
먼저 시간 단계 270개를 가진 시계열의 특징을 생성
특징 생성에 사용된 함수의 이름을 ft 로 줄였다
times = []
values = []
for idx, row in words_features.iterrows():
values.append(np.histogram(row.values, bins=10, range=(-2.5, 5.0))[0] + .0001) ## cesium seems not to handle 0s
times.append(np.array([i for i in range(9)]))
features_to_use = ["amplitude",
"percent_close_to_median",
"skew"
]
featurized_hists = featurize.featurize_time_series(times=times,
values=values,
errors=None,
features_to_use=features_to_use,
scheduler = None)
featurized_hists.to_csv('./featurized_hists.csv')
np.histogram() 에 전달된 인수로 모든 히스토그램이 같은 구간 개수, 구간마다 같은 범위의 값들로 구성되도록 한다.
이렇게 하면 모든 히스토그램이 같은 범위의 구간 값을 가져서 이들을 직접 비교할 수 있으며 시계열 특징 생성 작어베 사용될 시 이 값들이 시간의 축으로써 활용됩니다
이러한 일관성 없이는 히스토그램 간 비교가 불가능하여 생성된 특징이 무의미해진다
마지막으로 서로 다른 방식으로 얻은 특징들을 결합한다
features = pd.concat([featurized_words.reset_index(drop=True), featurized_hists], axis=1)
시간을 인식하는 거리 측정법
클러스터링 분석 시 거리 지표를 선택해야 한다
비시계열 데이터에 대한 표준 클러스터링 분석과 마찬가지로 방금 얻은 시계열 특징에 다양한 표준 거리 지표를 적용할 수 있다
이번 절에서는 시계열 간의 유사성 측정 문제를 다루기 위한 거리 지표를 정의한다
이러한 목적의 거리 지표 중 가장 잘 알려진 것은 동적시간왜곡(DTW) 이다
DTW 는 단어 투영과 같이 전체적인 모양이 가장 중요한 특징인 시계열의 클러스터링에 적합하다
이 기법의 이름은 시간축에 따라 시계열을 정렬하고 모양을 비교하는 시간적 '왜곡' 에 의존하는 방법론으로부터 영감을 받는다
글보다는 그림이 동적시간왜곡의 개념을 훨씬 더 잘 전달한다
표시된 두 곡선 사이의 점들 간 최상의 정렬을 찾아서 두 곡선의 모양을 비교하기 위해서 시간축 x 이 왜곡(확장 또는 축소) 된다
다른 곡선과 비교해서 한 곡선의 시간축상 실제 시간 값은 이 알고리즘의 표준 형식에 적합하지 않다
나노초 단위로 측정된 시계열과 수천 년 단위로 측정된 시계열을 비교할 수 있다
이 알고리즘의 목적은 지나간 시간의 양을 생각하는 것보다는 알고리즘의 시각적 '모양'을 비교하는 것에 가깝다
즉 '시간' 이란 고유한 시간보다는 x축을 따라 균등한 간격으로 정렬된 점들이라는 일반화된 의미가 있다
DTW 의 규칙은 다음과 같다
용량상 다음 장에서
'시계열 분석 > Practical TIme Series Analysis' 카테고리의 다른 글
| 10)시계열 딥러닝 ANN (0) | 2022.11.04 |
|---|---|
| 8)시계열을 위한 머신러닝2 (0) | 2022.10.31 |
| 6)시계열 특징의 생성 및 선택 (0) | 2022.10.26 |
| 5)시계열의 통계모델3 (0) | 2022.10.26 |
| 5)시계열의 통계모델2 (0) | 2022.10.25 |


